Parallelograms are fascinating geometric shapes that can be found everywhere, from the pages of a book to the foundations of buildings. Calculating the area of a parallelogram is a fundamental skill in geometry and mathematics, and it is often encountered in various real-life scenarios. In this article, we will dive into the world of parallelograms, exploring what they are, how they work, and, most importantly, how to calculate their area with ease.
What is a Parallelogram?
Before we delve into the area calculation, it’s essential to understand what a parallelogram is. A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides that are parallel and equal in length. In simple terms, the opposite sides of a parallelogram never meet, and they have the same length. This unique characteristic sets parallelograms apart from other quadrilaterals, like rectangles or rhombuses.
Understanding the Anatomy of a Parallelogram
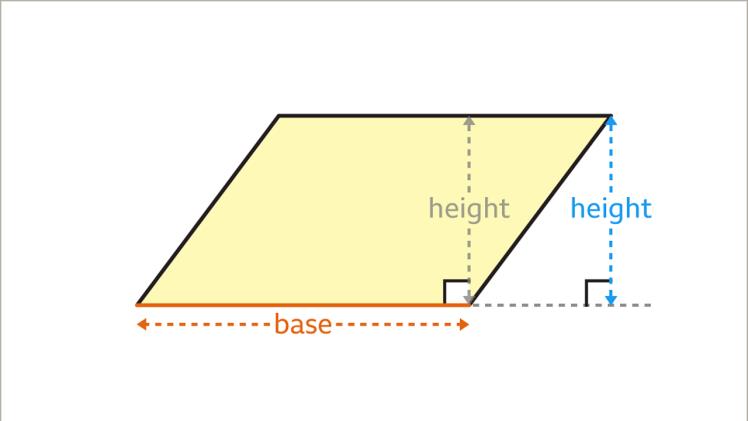
To calculate the area of a parallelogram, it’s vital to familiarize ourselves with its key components. The critical elements of a parallelogram are its base, height, and the two pairs of parallel sides. The base is one of the sides, typically the one upon which the parallelogram stands. The height is the perpendicular distance between the base and the opposite side.
The Formula for Calculating the Area of a Parallelogram
The area of a parallelogram can be calculated using a simple formula:
Area = Base x Height
It’s a straightforward multiplication of the base and the height. Keep in mind that the height must be the perpendicular distance between the base and the opposite side. The base can be any of the sides, but it’s important to ensure the height is drawn from that base.
Step-by-Step Guide to Calculating the Area of a Parallelogram
Let’s break down the process into simple steps to make it even more accessible:
Identify the Base: Choose one of the sides of the parallelogram as the base. It’s essential to be consistent in your choice to avoid any errors in the calculation.
Determine the Height: The height is the perpendicular distance from the chosen base to the opposite side. To do this, draw a straight line from the chosen base to the opposite side. Ensure this line forms a 90-degree angle with the base.
Measure the Base and Height: Use a ruler or any measuring tool to find the length of the base and the height. Ensure your measurements are accurate for precise results.
Calculate the Area: Plug the values of the base and the height into the formula: Area = Base x Height. Multiply the length of the base by the height to find the area of the parallelogram.
Express the Area: The area of the parallelogram is typically measured in square units (e.g., square inches, square centimeters, etc.). So, ensure your base and height are in the same units before multiplying.
Example Calculation:
Let’s take a practical example to demonstrate the process. Imagine you have a parallelogram with a base of 8 inches and a height of 5 inches. To calculate its area:
Area = Base x Height Area = 8 inches x 5 inches Area = 40 square inches
The area of the parallelogram is 40 square inches.
Special Cases:
Right-Angle Parallelogram: If your parallelogram is a right-angle parallelogram (a parallelogram where one angle is 90 degrees), you can use the formula for the area of a rectangle: Area = Length x Width, as the opposite sides are perpendicular.
Rhombus: A rhombus is a type of parallelogram with all sides of equal length. To find the area of a rhombus, you can use the formula: Area = (Diagonal1 x Diagonal2) / 2. Here, Diagonal1 and Diagonal2 are the lengths of the two diagonals that cross each other.
Non-Standard Parallelograms: If you encounter a parallelogram that isn’t perfectly aligned or doesn’t follow standard geometric conventions, you may need to apply additional geometry principles to calculate its area accurately.
In conclusion, calculating the area of a parallelogram is a fundamental skill in geometry and mathematics. Understanding the base, height, and the simple area formula (Area = Base x Height) is key to mastering this concept. By applying these principles, you can unlock the mysteries of parallelograms and use this knowledge to solve real-world problems, from calculating the area of a field to understanding the geometry of architectural structures.